ESE446: Robotics Dynamics and Control Final Project � Adith Jagadish Boloor

Objective:� The objective of the project is to gain understanding of various robot manipulator design tools and characteristics.� Through the use of an example we want to demonstrate the understanding of the Jacobian, robot dynamics, trajectory, and manipulator control.� The example to be used will be the 3R planar robot describe in the figures illustrated below.

 

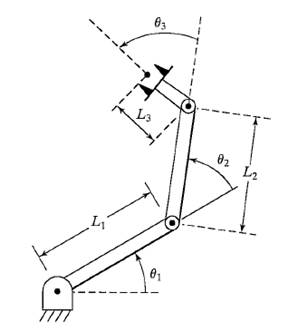
Figure 1: 3R Planar Robot

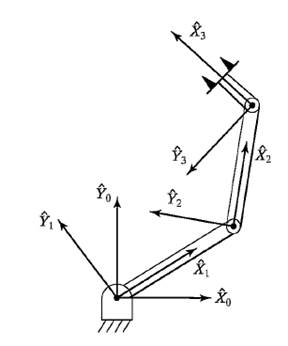
Figure 2: Frame layout for 3R Planar Robot

 

 

Task-1: Robot Simulation

Table 1: DH Link table for 3R Planar Robot

 

1

0

0

0

1

0

2

0

0

1

0

3

0

0

1

0

 

4

0

0

0

1

0

 

The Denavit�Hartenberg (DH) parameters shown in table one is one way we can go about describing the kinematics (position) of the robot arm. The parameters are described as follows:

�         �� angle about the common normal, from the previous z-axis to the new z-axis

�         �� length of the common normal (in this case, the length of each non-prismatic link)

�         d - �offset along previous z-axis {\displaystyle z}to the common normal

�         �� angle about the previous z-axis from the previous x-axis to the new x-axis{\displaystyle \theta \,}

 

The transformation matrix is given by:

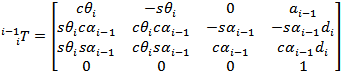
Note that the �s� denotes sine and �c� denotes cosine. The transformation matrix is a mathematical representation of the pose for a particular link (i) of a robot, with respect to the previous link (i-1). The 3x3 sub-matrix of the transformation matrix is called the rotational matrix:

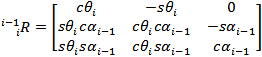
The rotational matrix is a mathematical representation of the angle of the link with respect to the previous link.

The 4th column (neglecting the 4th row) of the transformation matrix is the position vector as shown below:

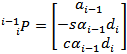
The position vector is a mathematical representation of the position of the link with respect to the previous link.

Using the DH matrix, and the generalized formula for the transformation matrix shown above, the transformation matrices can be calculated for each link. Note that zero is the base �link�.

The most important property of transformation matrices is that the pose of a link with respect to the base can be calculated with ease using matrix multiplication as follows:

The same method can be used to calculate the rotation matrices

T1 (Task-1) Derive dynamic equation for manipulator.

The dynamic equation for any robot is given by the following equation which governs the torque applied at the actuators and the external forces applied to the manipulators, which is got from the Lagrangian, which simply applies the conversation of energy principle.

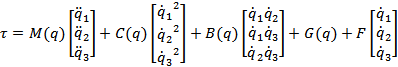
�         �� tau vector (forces applied at the actuators)

�         �� mass matrix (mass distribution as a function of manipulator pose)

�         �� centrifugal matrix

�         �� Coriolis matrix

�         � gravitational force vector

�         � kinetic frictional force coefficients

�         �� generalized position of a joint

�         �� angular velocity of joint i

�         �-� angular acceleration of joint i

 

The Mass Matrix:

To calculate the mass matrix, we must first calculate the velocity and angular velocity Jacobians of each joint. In simple words, a Jacobian is a matrix whose elements show how each joint�s spatial properties change with each other.

The velocity Jacobian is given by:

The q�s represent the angular position of each respective link. �is the position vector of the center of mass for each link. Note that each Jv will be a 3x3 matrix. This is given by:

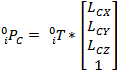
Where �is the center of mass of that link in its zero (q1, q2 q3 = 0) position. In our case, the center of mass vector looked like the following for each link.

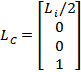
Where �is the length of the i link. This assumes that the mass is uniformly distributed along the links.

The angular Jacobian is given by:

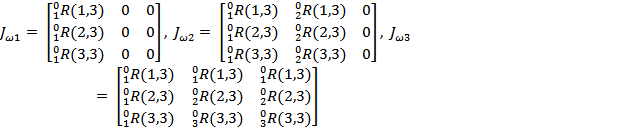
Here (i,3) etc., refers to the i�th element of the third column of the rotation matrix. We use this because the third column of the rotational matrix holds the angular information for that link.

To represent the mass distribution relating to the angular velocity, we also need the inertial properties of the robot. The inertial matrix (also called Intertial tensor) for each joint is given by:

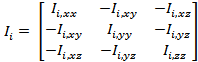
�represents the moment of inertia about the x axis for each link, and same goes for y and z. �represents the product of inertia between the respective axes. Since our robot is a planar robot in the x and y coordinate frame, we will have only . The other moments will be zero.

Now to calculate the mass distribution with respect to velocity and angular velocity for each link, we have:

 

The overall mass matrix is given by:

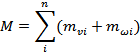
The Centrifugal matrix (C) and Coriolis (B) matrix:

Like their name state, the centrifugal matrix represents the centrifugal forces, and the Coriolis matrix represents the Coriolis force experienced by the system.

The centrifugal matrix for a 3 link RRR robot is given by:

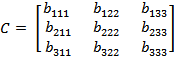
And the Coriolis matrix is given by:

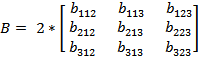
Where, �(known as Christoffel Symbols) is given by:

And

Where �is the ij element of each matrix. Fun.

 

The gravity matrix:

The gravity matrix shows the forces experienced by the robot in the negative y-direction (because of acceleration due to gravity).

 

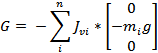
�         �� velocity Jacobian

�         - mass of each link

�         �� acceleration due to gravity (+9.81m/s2)

The Friction vector:

Ideally we would be using both static and dynamic (kinetic) friction. But to keep it simple, we will be using only dynamic friction, because we are more interested in what happens to the robot during motion. Note that friction is very important in the simulation of this robot. Because without it, there is no resistance for each joint and they will behave sporadically.

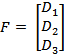
Where �is the coefficient of dynamic friction of each link.

Tau vector:

After calculating all the vectors and matrices, we can calculate the tau vector that comprises the forces at each joint. Why do we call it tau instead of force? Who knows?

Just to recap, the formula is:

�

 

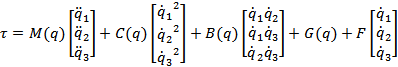
T1. Solve equations for acceleration and use these to create state-space simulator.

We simply use the state space equation mentioned previously to solve for the accelerations of each joint.

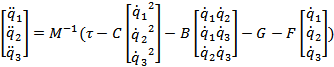
Check attachment (vectors_qpp_tau.txt) for all the matrices and acceleration solutions.

 

T1. Use robot manipulator initial angles of 10, 20, and 30 degrees respectively. DONE.

T1. Use individual link lengths of 4, 3, and 2 meters respectively. DONE

T1. Use individual link masses of 20, 15, and 10 kg respectively. DONE

T1. Use a-axis inertial values of 0.5, 0.2, and 0.1 kg-m2 respectively. DONE

T1. Demonstrate dynamics of the robot through simulation.

The Simulink model looks like the following for T1:

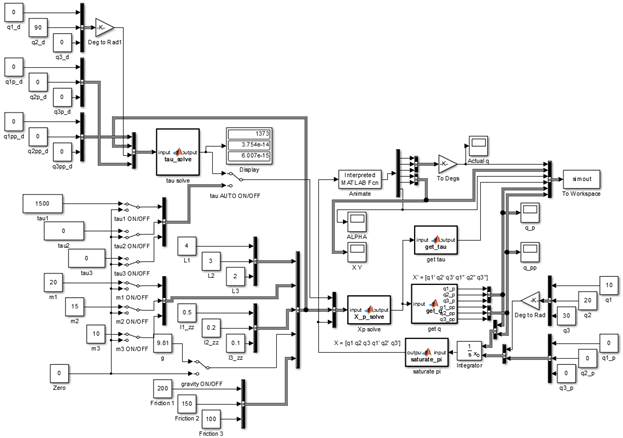
Figure 3: Simulink Model for Task1

Notice that all parameters are changeable. The scopes can be used to check how each parameter changes with the robot animation. On the right side of the image you can see that the initial angles are set as 10, 20 and 30 degrees respectively.

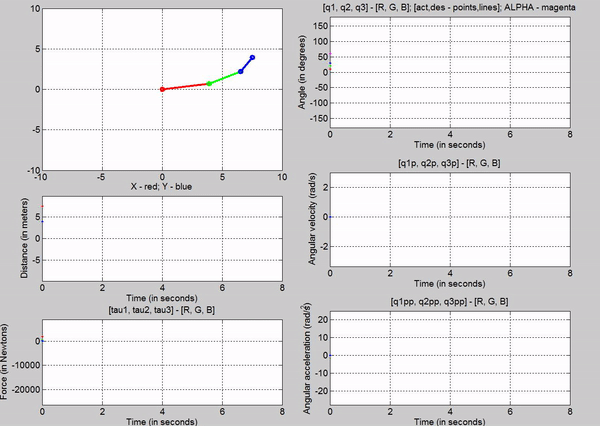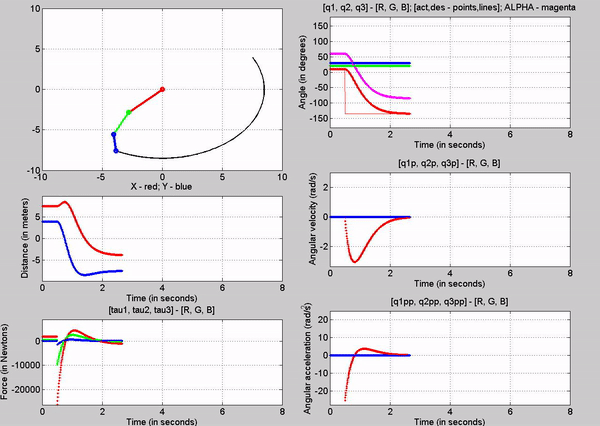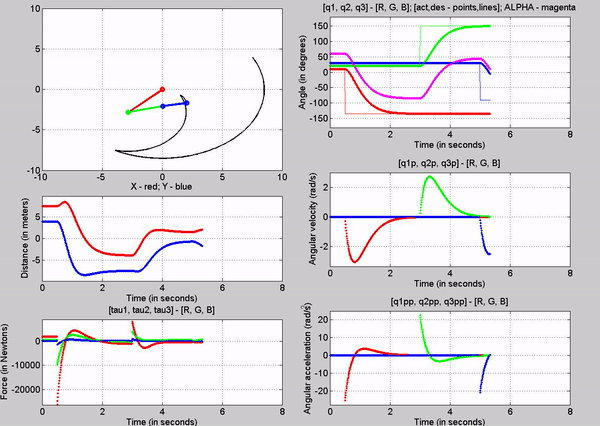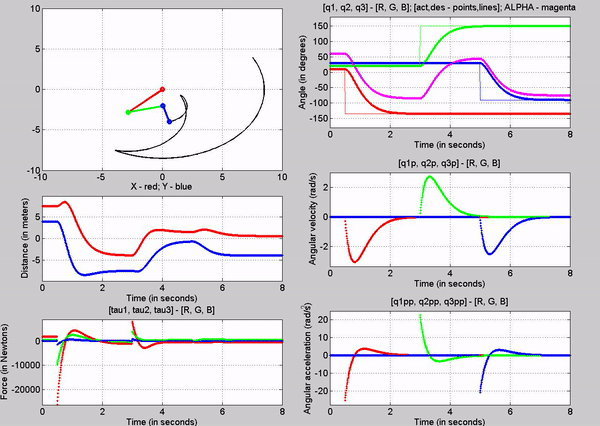
1.      No actuator torque, no gravity

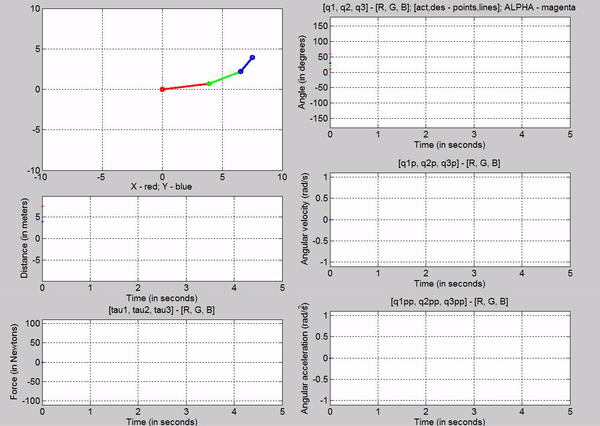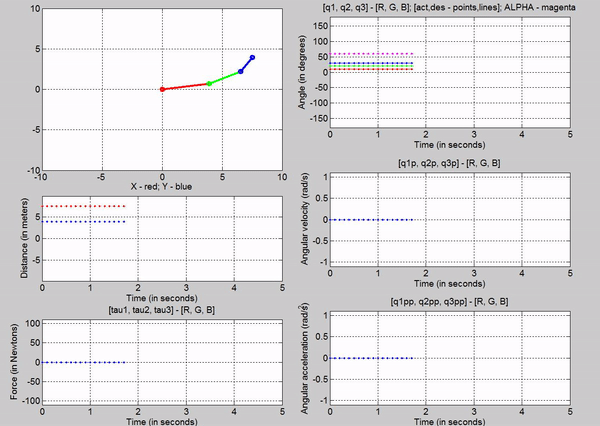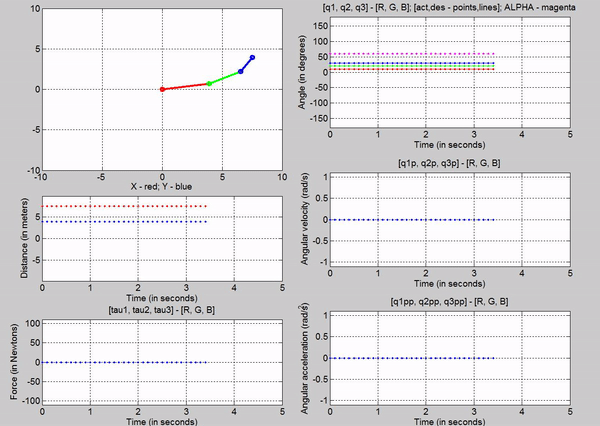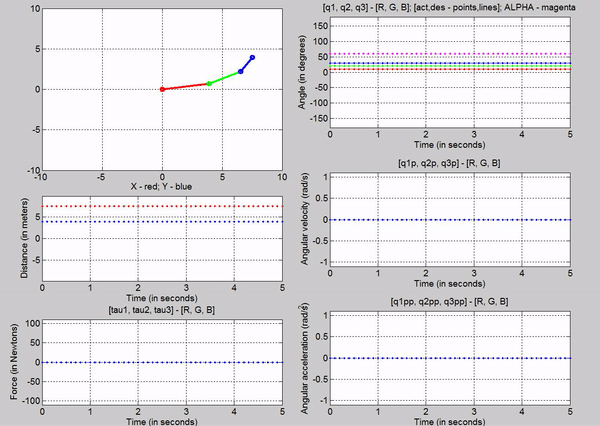
Figure 4: Simulation - [tau1, tau2, tau3] = [0, 0, 0]; g = 0

The arm stays still because there are no internal or external forces acting on it.

Created gif using: https://ezgif.com/video-to-gif/

Converted avi to mp4 using: http://convert-video-online.com/

2.      No actuator torque, with gravity

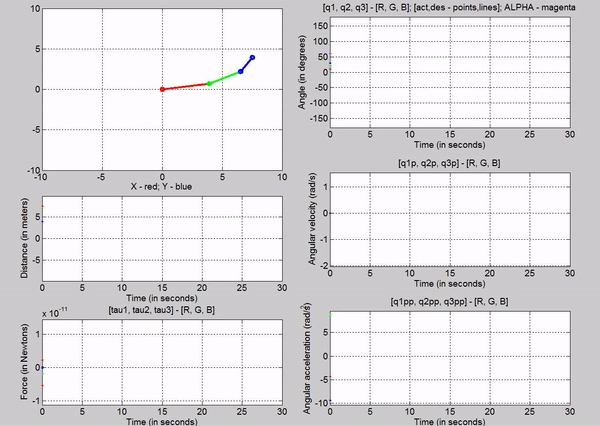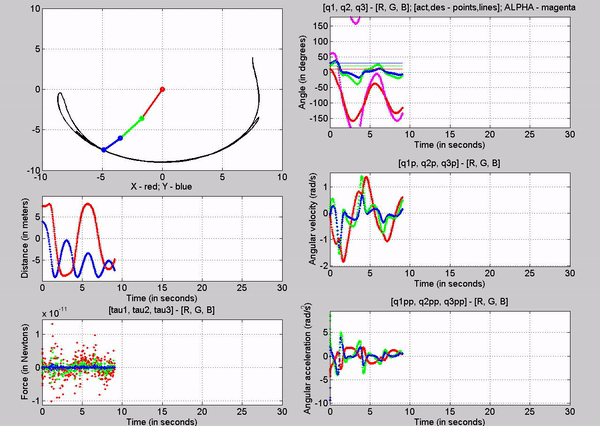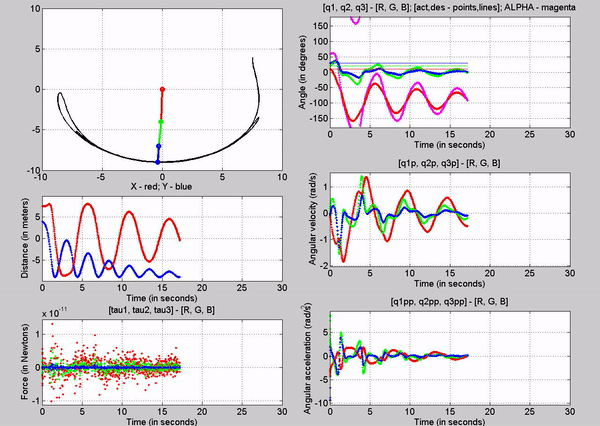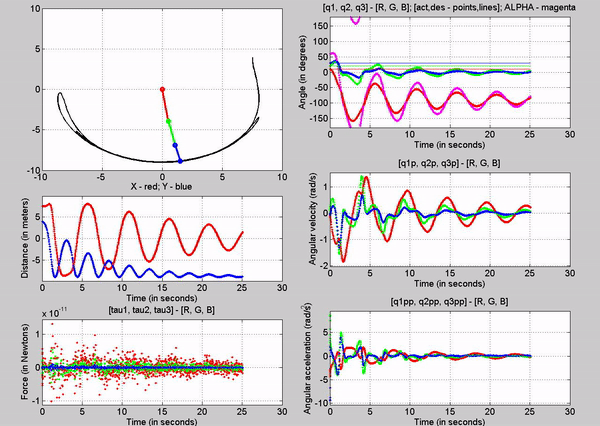
Figure 5: Simulation - [tau1, tau2, tau3] = [0, 0, 0]; g = 9.81m/s2

Here the arm falls downwards, and oscillates about negative 0 in the y direction because gravity is the force acting on it, which is in the negative y direction.

3.      Joint-1 actuator torque in order to provide equilibrium, with gravity

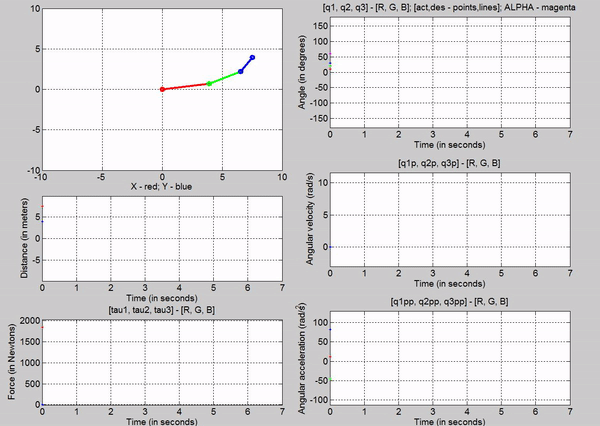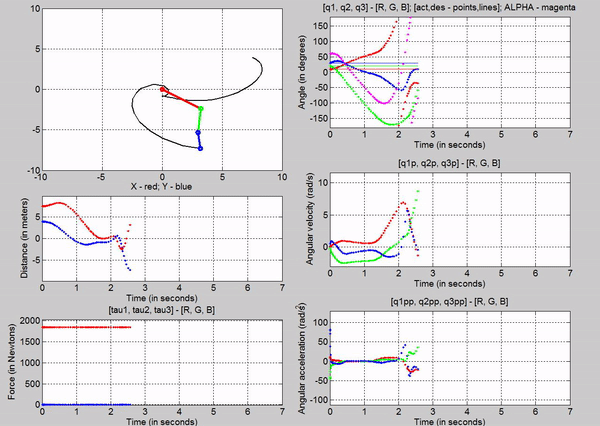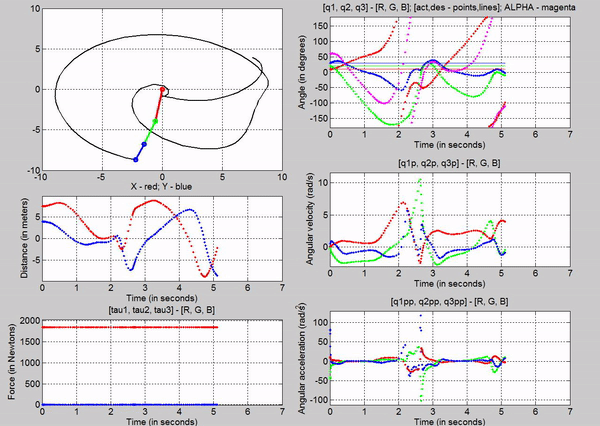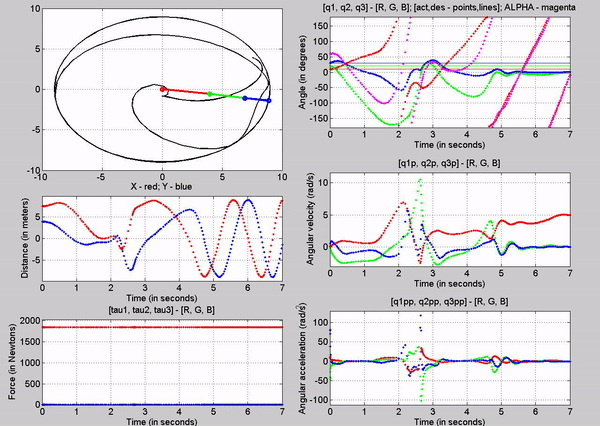
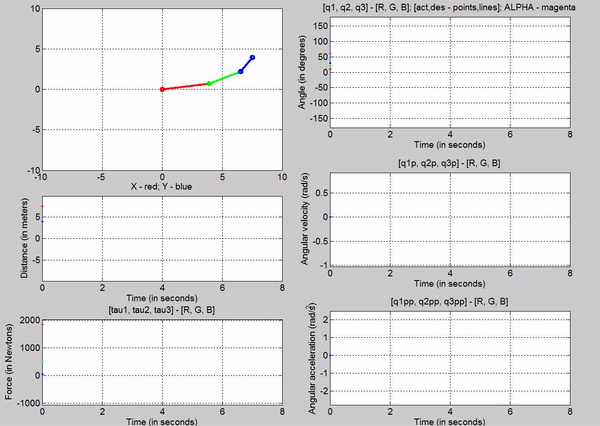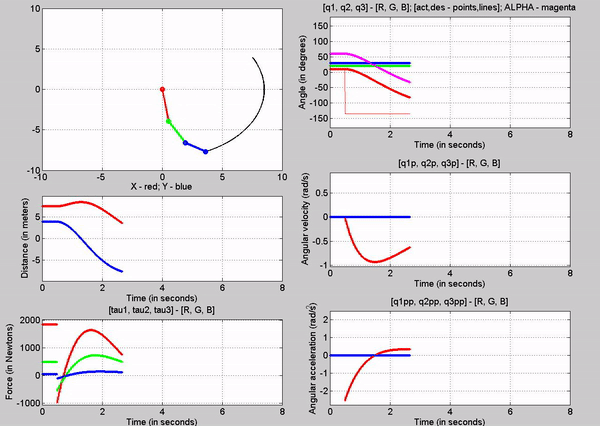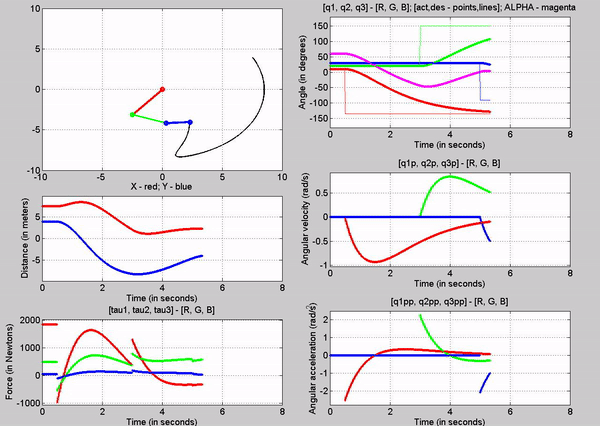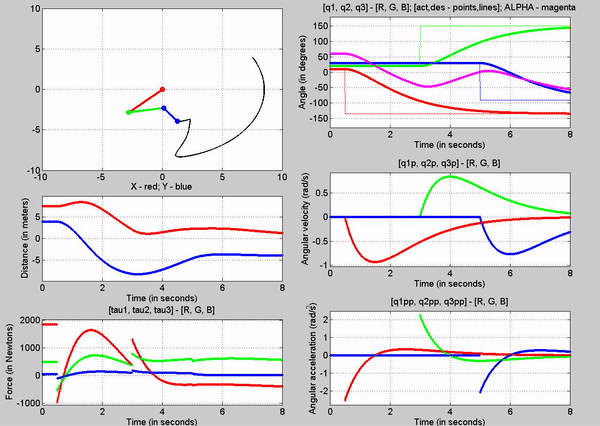
Figure 6: Simulation - [tau1, tau2, tau3] = [1845, 0, 0] N; g = 9.81 m/s2

The tau values for the joints are:

�         Joint 1 � 1845 N

�         Joint 2 � 0 N

�         Joint 3-� 0 N

The force chosen at joint 1 is based on trying to establish equilibrium for the links at 10, 20 and 30 degrees respectively. The taus were calculated using the Lagrangian equation derived before, setting the velocities and accelerations to zero. Observe that just for a brief second, link 1 stays at 10 degrees before the motion of other links make the robot become unstable. This is because we are attempting to balance the robot with a constant torque in an open-loop control method.

4.      Joint-1 and Joint-2 actuator torque in order to provide equilibrium, with gravity

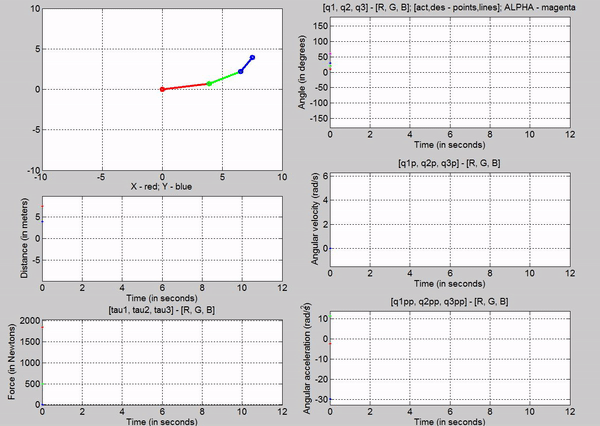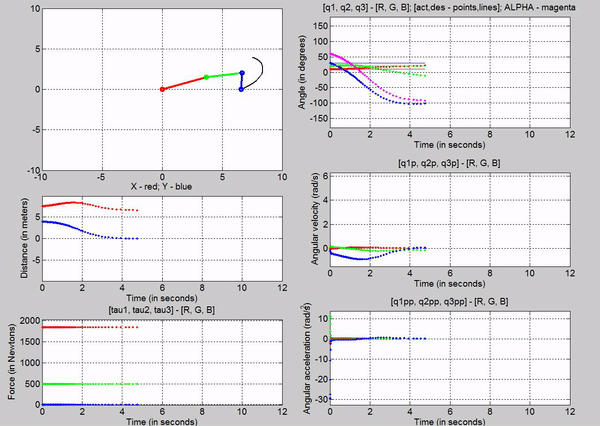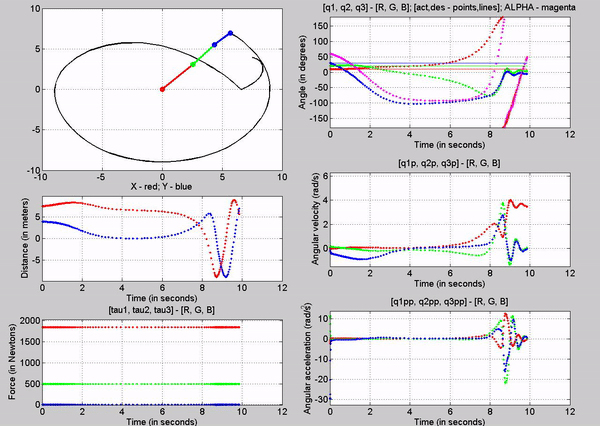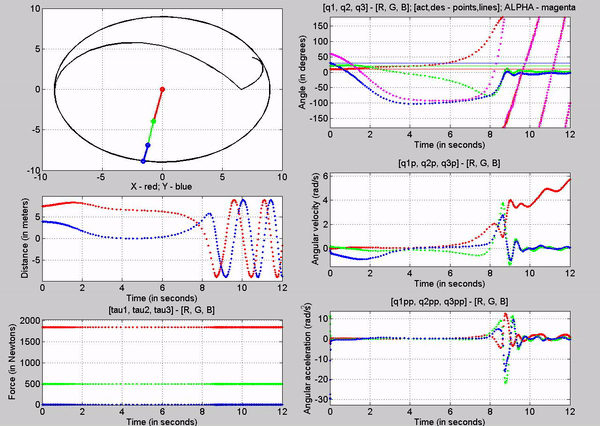
Figure 7: Simulation - [tau1, tau2, tau3] = [1845, 495.1, 0] N; g = 9.81 m/s2

The tau values for the joints are:

�         Joint 1 - 1845 N

�         Joint 2 - 495.1 N

�         Joint 3-� 0 N

The forces chosen at joint 1 and 2, are based on trying to establish equilibrium for the links at 10, 20 and 30 degrees respectively. Observe that just for a brief second, links 1 and 2 stay at 10 and 20 degrees respectively before the motion of other links make the robot become unstable. Also note that this time the robot stays in equilibrium a bit longer than while we used torque at only one joint. Again this is because we are attempting to balance the robot with a constant torque in an open-loop control method.

 

5. Joint-1, Joint-2, and Joint-3 actuator torque in order to provide equilibrium, with gravity

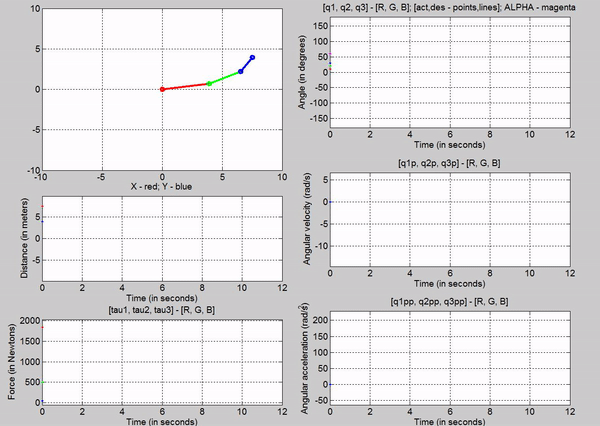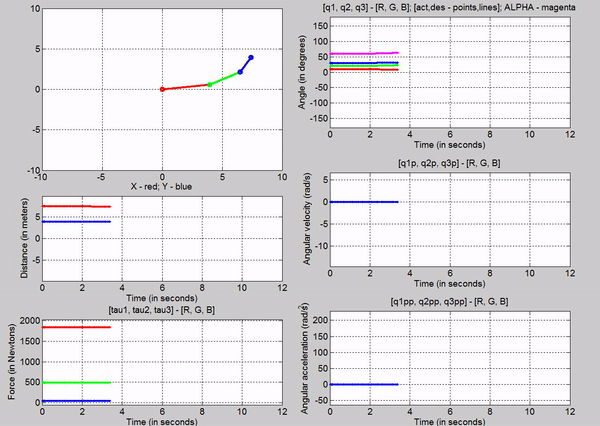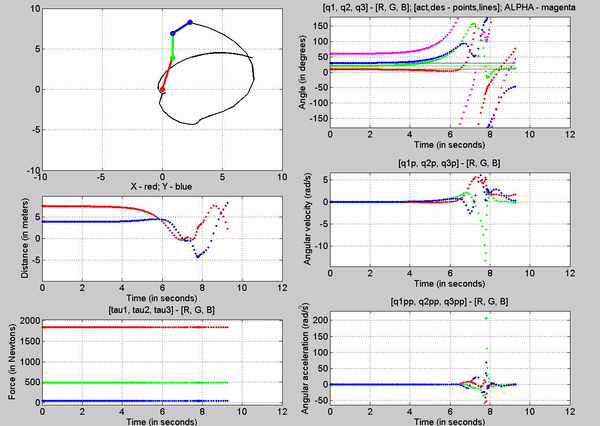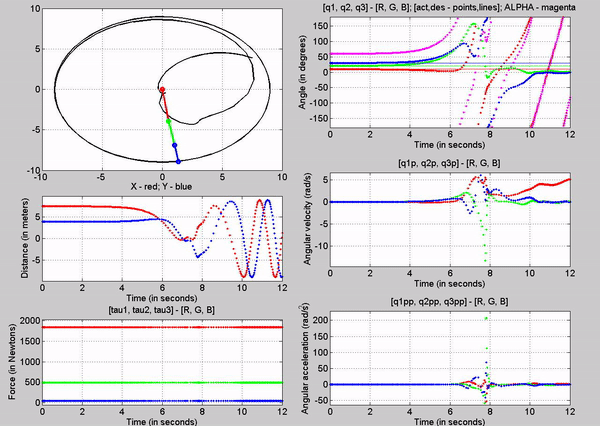
Figure 8: Simulation - [tau1, tau2, tau3] = [1845, 495.1, 49.05] N; g = 9.81 m/s2

The tau values for the joints are:

�         Joint 1 - 1845 N

�         Joint 2 - 495.1 N

�         Joint 3-� 49.05 N

 

The forces chosen at joint 1, 2 and 3, are based on trying to establish equilibrium for the links at 10, 20 and 30 degrees respectively. Observe that this time, the robot stays in equilibrium a lot longer. However it becomes unstable because of tiny changes in position of the links (most like caused because of the forces� precision). Again this is because we are attempting to balance the robot with using open-loop control.

 

T1. All simulations should present graphs of x,y, and alpha end-effector positions vs. time.

Did one better. Added tau, q, q� and q�� vs time graphs as well

T1. Include any other graphs, gif�s, etc. which you deem necessary to describe the demonstration. DONE

 

 

Task-2 Robot simulation � with control partitioning

T2 (Task 2) Design a closed loop system by partitioning the robot dynamics into model-based and servo-based dynamics.

For task 2, we are incorporating a position and velocity controlled closed loop.

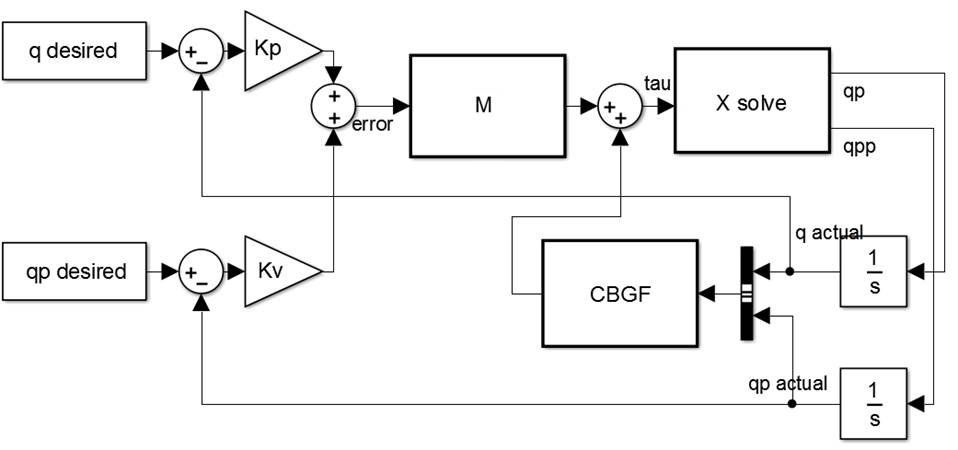
Figure 9: Closed loop control

Figure 9 shows us how the desired and actual position and velocity are being multiplied by their respective gains (Kp and Kv), and summed up. Kp and Kv are essentially the weightage we give for these error signals. This gives us the overall error in q. This is fed into the mass matrix (M) and summed up with the centrifugal (C), Coriolis (B), gravity (G) and friction (F) matrices/vectors to give us the forces (tau). Using the tau, we can solve for the accelerations (qpp) using the Lagrangian equation mentioned earlier. The output of this being the acceleration and the velocity (qp) go through an integrator to get the actual velocity and position of the robot. These values are used for the CBGF calculations and for subtracting them from the actual position and velocity respectively. The control loop tries to get the error to zero. The Kp tells us how fast it will try to decrease the error, while the Kv helps damped the motion as the error is decreased. A good place to start Kp is at 1, and increase it. Kv is typically twice the square root of Kp.

T2. Simulate the system by setting the initial joint angles to 10, 20, and 30 degrees respectively. Explain what happens during the simulation.

The Simulink model for task 2 is as follows:

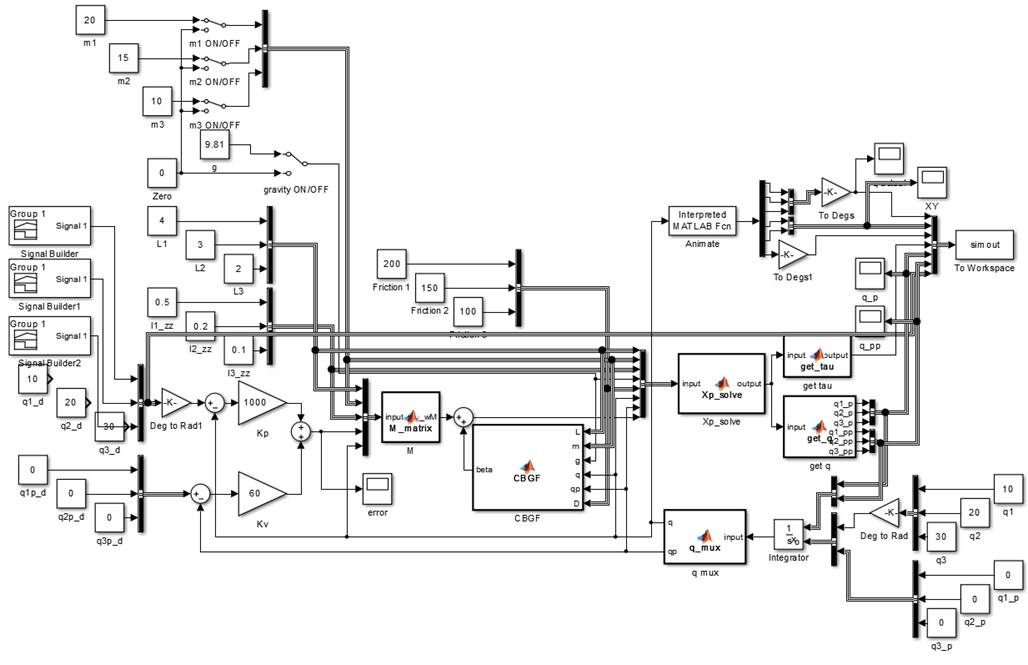
Figure 10: Task 2 Simulink Model

 

The simulation will be explained in the subsequent subsections.

T2. Add joint-position control by adding an input vector which represents the joint desired positions. DONE

T2. Simulate the system with the above initial angles and appropriate input command angles. DONE

T2. One joint at a time, apply a step input change to the command angle. Monitor the response of the system by examining the error signal.

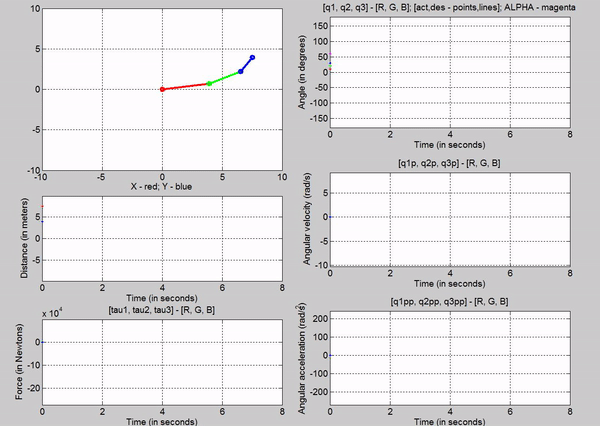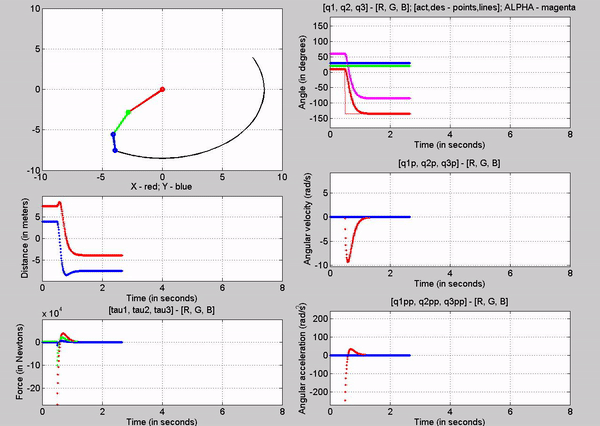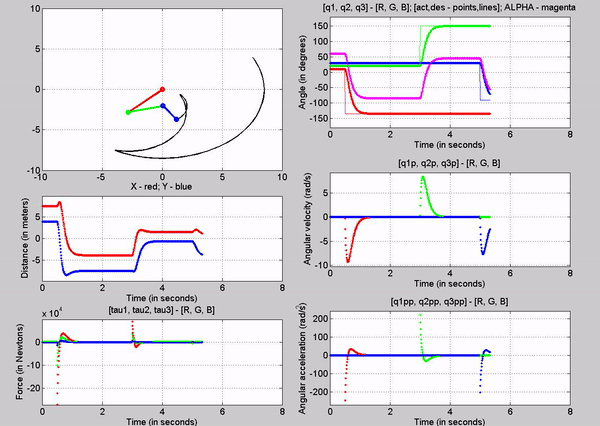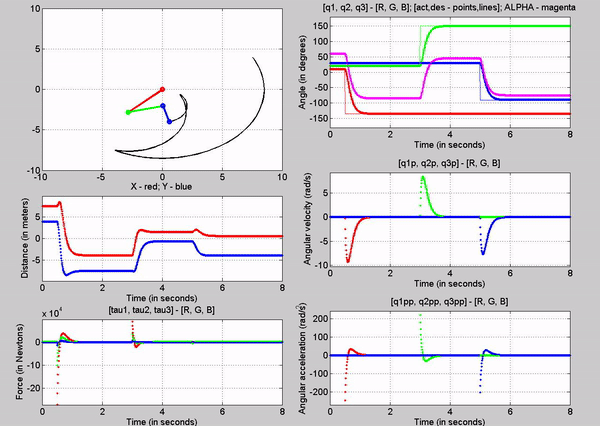
A simple demo was done incorporating the above closed loop control with Kp = 10 and Kv = 6. Several desired positions (or command angles) were used to check the effectiveness of the control as you can see in the following animation.

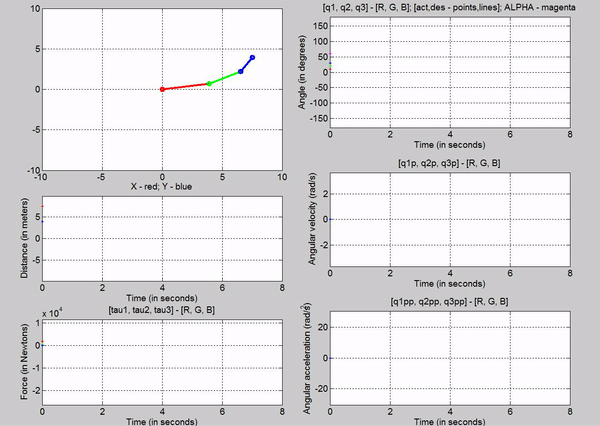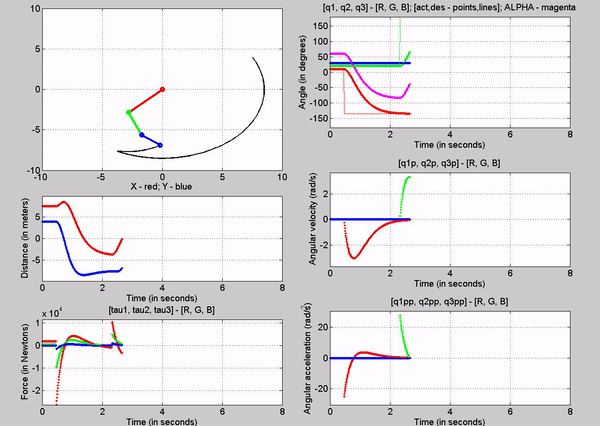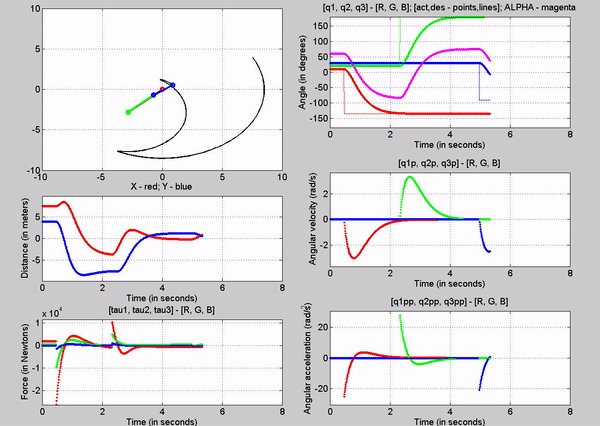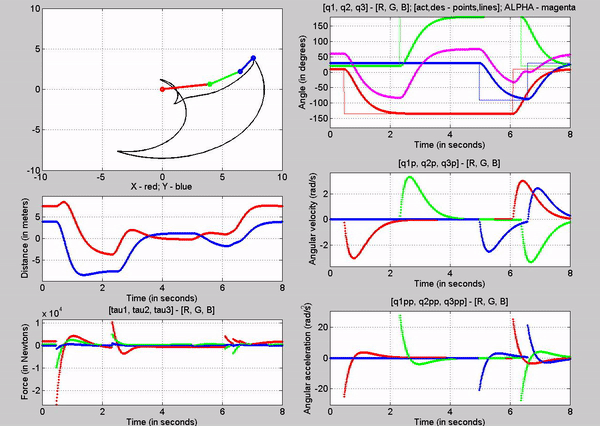
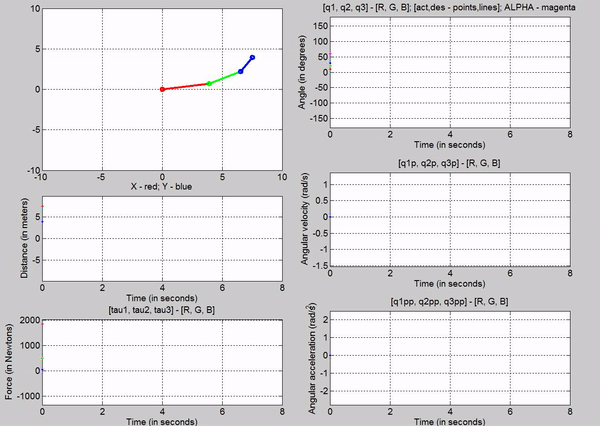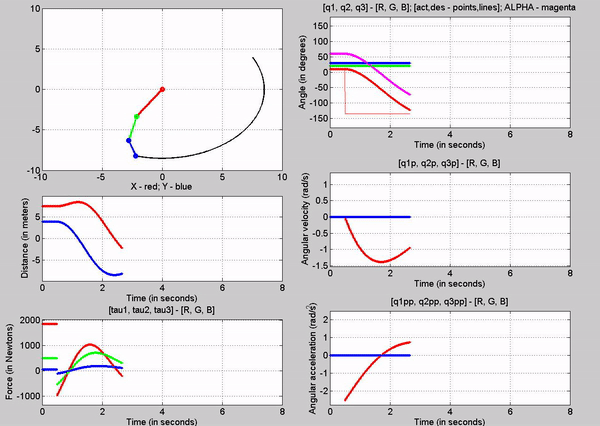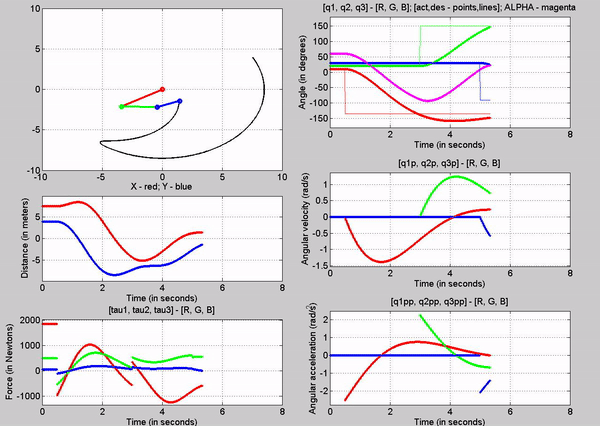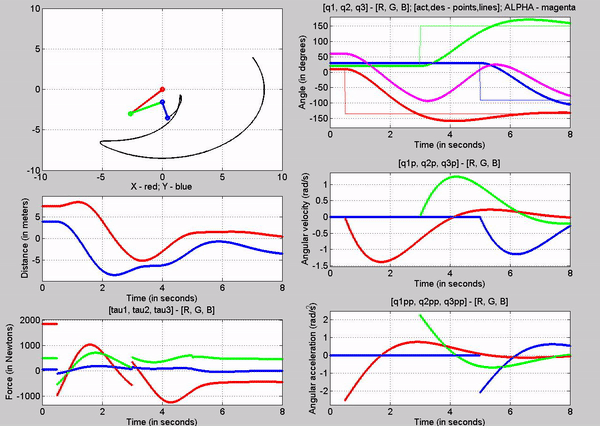
Figure 11: Animation - Kp = 10 Kv = 6 for different command angles

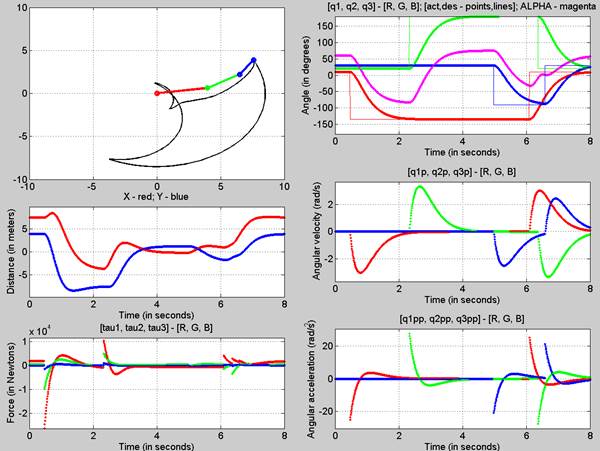
Figure 12: Final Pose - Kp = 10, Kv = 6

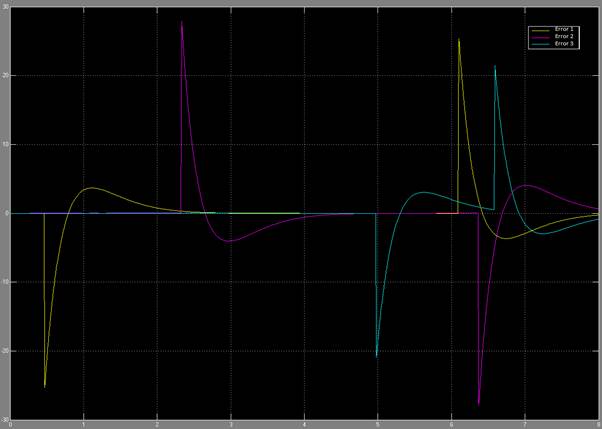
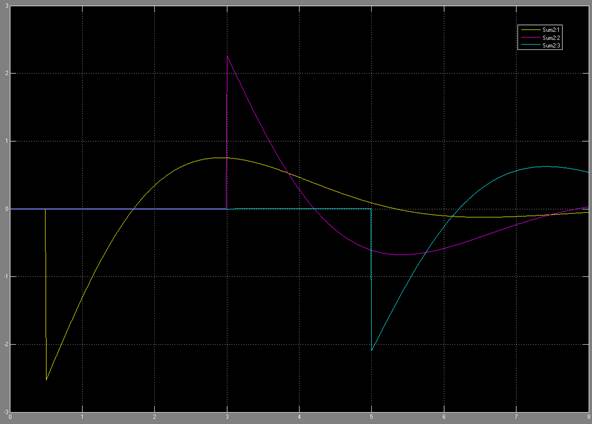
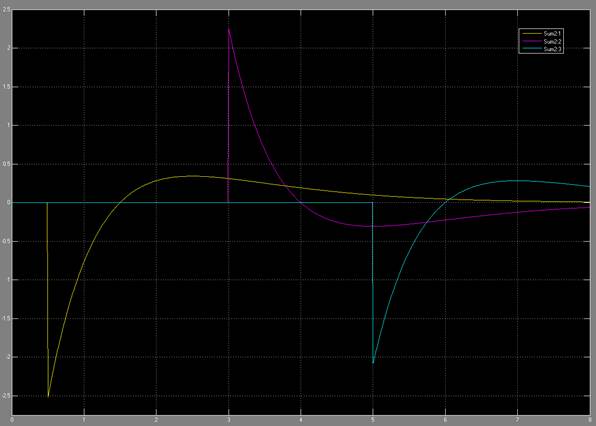
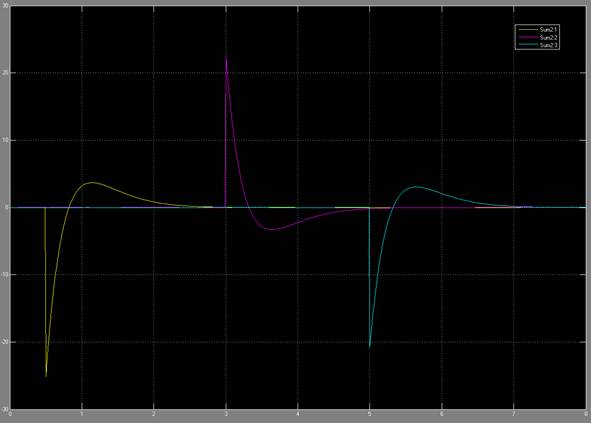
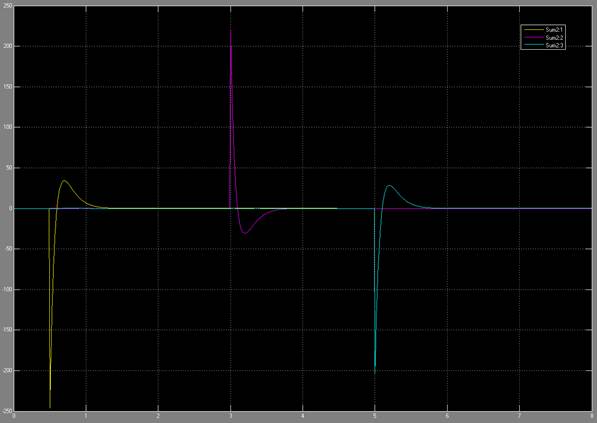
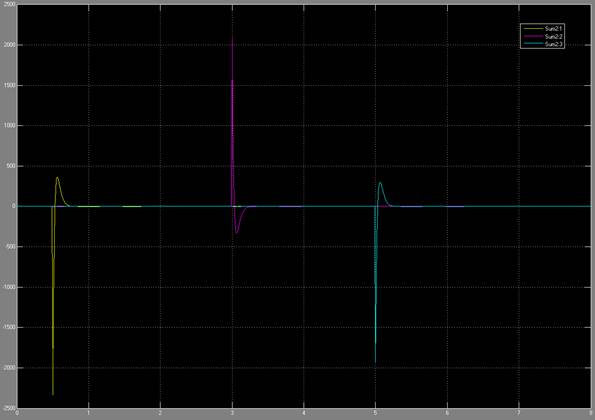
Figure 13: Error signal through the changes in command angle

Figure 11 shows the animation of the robot as it goes to the input desired angles. You can see from the q subplot (figure 12) how the robot moves to those angles. The response looks like a first order system. In figure 13, you can see the error signals, which we try to get to zero using the closed loop control. We can see that there is some over shoot for all the joints. This can be mitigated by choosing different kp and kv values.

T2. Experiment with various Kp gains (such as 1, 10, 100, etc.) and explain the results.

To run the same experiments for different gains, a signal builder was used that set the command angle for q1 to -135 degs at 0.5 seconds, q2 to 150 degs at 3 seconds and q3 to -90 degrees at 5 seconds each time.

Kp = 1; Kv = 1

��

Kp = 1; Kv = 2

�

Kp = 10; Kv = 6

�

Kp = 100; Kv = 20

�

Kp = 1000; Kv = 60

�

The higher the Kp value, the faster the response of the system is, i.e., the higher the gains, the faster the errors get driven to zero. Since this is a simulated system, we have no repercussions of using higher and higher gains, however in a real system the higher the gains, the more energy (in terms of voltage) you would need to supply. Additionally in a real system, using very high gains could damage components like gears and the motor.

T2. How does the rise time change? Talked about in the next subsection.

T2. Can you set the gain to give overshoot?

The following table is made from the data above for q1 to give us a better understanding of how rise time and overshoot varies with Kp and Kv.

Table 2: Kp, Kv vs Rise time and Overshoot

Kp

Kv

Rise time (s)

Overshoot > 5%?

1

1

2.5

YES

1

2

5.5

NO

10

6

2

NO

100

20

1

NO

1000

60

0.25

NO

 

We can observe that the rise time decreases with increasing Kp, provided the Kv matches it (~2xsqrt(Kp)). Gains can be set to create overshoot. A Kp with the Kv lesser than 2sqrt(Kp) will create overshoot. Kv helps to dampen the system, hence it would make sense that if it is too small, the system would oscillate.

T2. Does the system need different Kp values for each joint?

As can be observed from the system above, you do not necessarily need different Kp values for each joint to get a fast response without overshoot. However, if you wanted the responses for each joint to be different, they would need different gains.

T2. Does the step response look like a second order system?

No, as long as the Kp and Kv values match each other (Kv ~ 2sqrt(Kp)), the system looks like a first order system. However, if the Kv is too low, the system could behave as a second order system.

 

 

Task-3: Robot simulation � path trajectory

Most industrial robot paths are programmed by teaching desired points along the path. This is done by using the teach pendant to maneuver to some desired point and orientation and then capturing the joints coordinate values. Given these joint coordinates and some desired time line we can create a reasonable trajectory through these points.

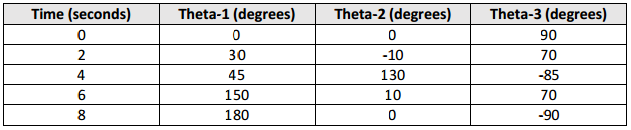
Given: The following timeline data

T3. (Task 3) Create a spline fit curve through each set of points for each joint. Make sure the starting and ending slopes of the trajectory (joint velocity) are zero. (Use the spline function in MATLab).

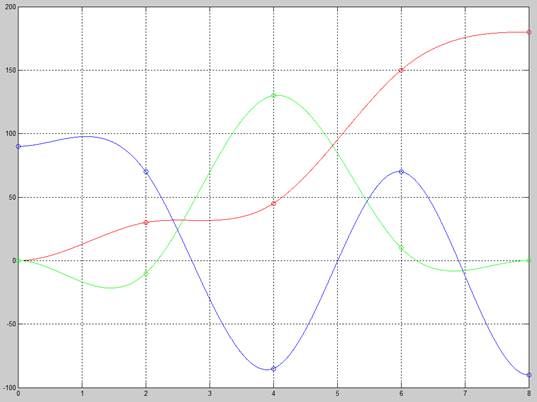
Figure 14: Cubic splines for q1, q2 and q3 (R, G, B)

Write a function to feed the three trajectory curves to your RRR robot simulator. DONE

Set initial angles of system to match those at time zero and simulate the path for 8 seconds. DONE

The following trajectory animations use Kp = 1000 and Kv = 60

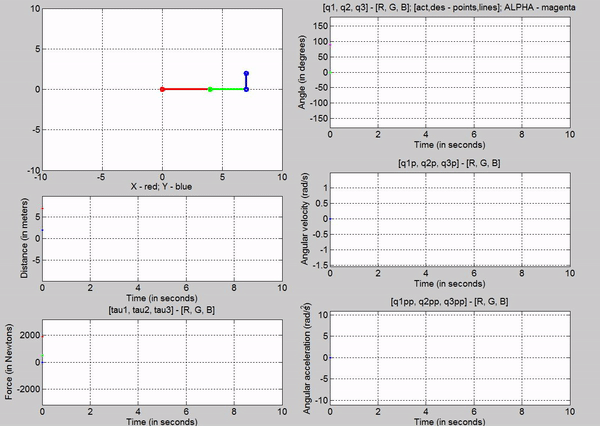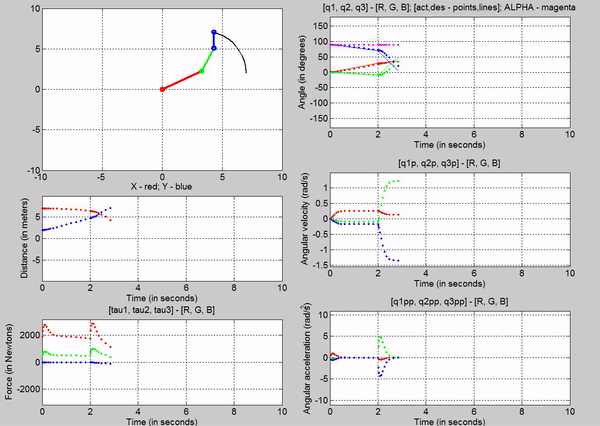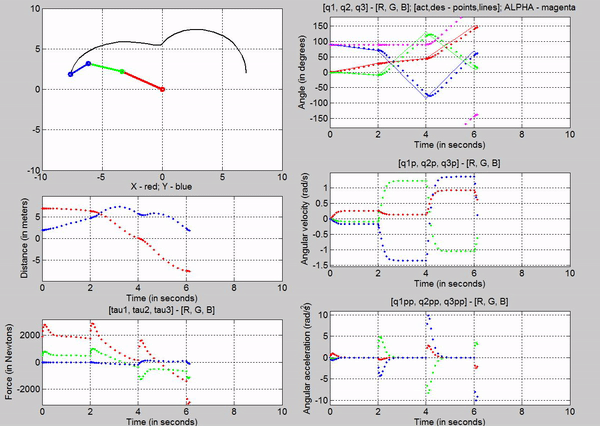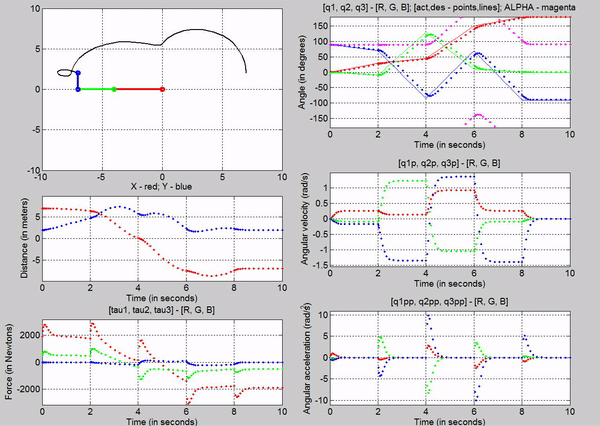
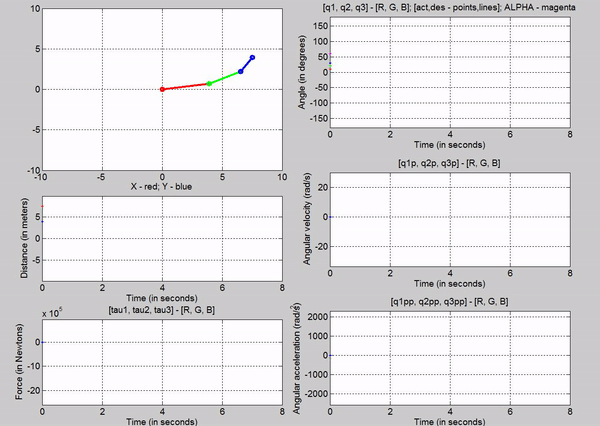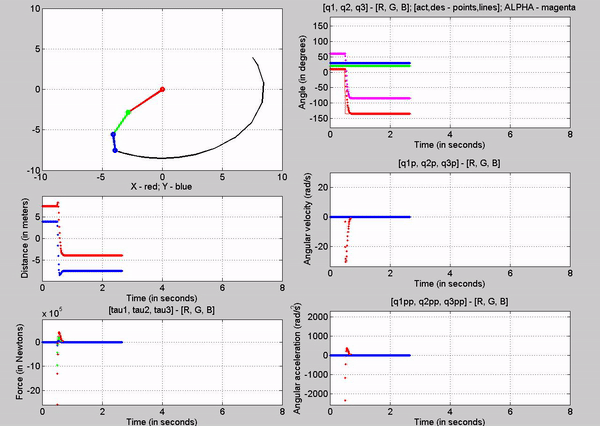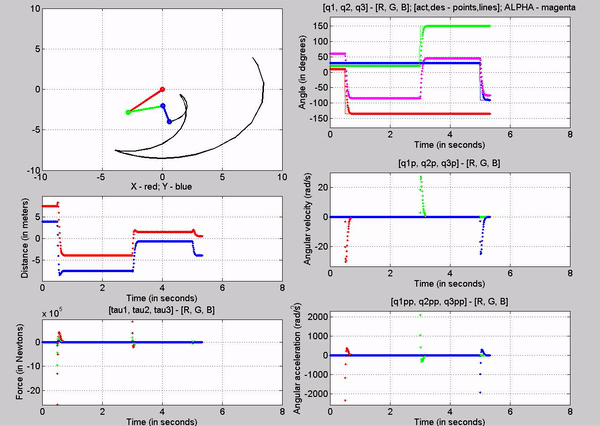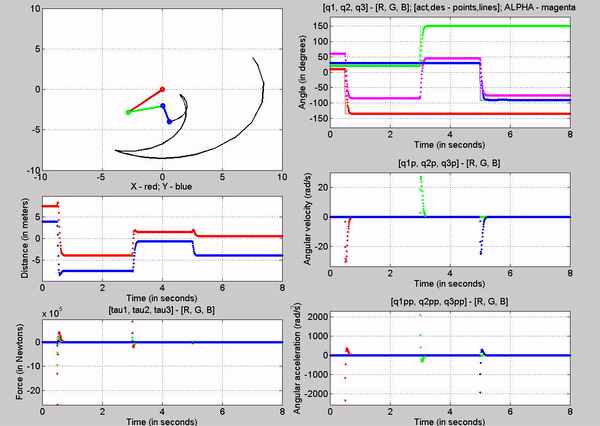
Figure 15: Trajectory follower using Signal Builder

Figure 15 was the result of using a signal builder. The signal for q1 looked like the following:

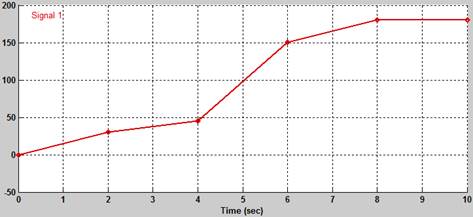
Figure 16: Signal Builder for q1

The following figure shows the animation using the spline function in MATLAB.

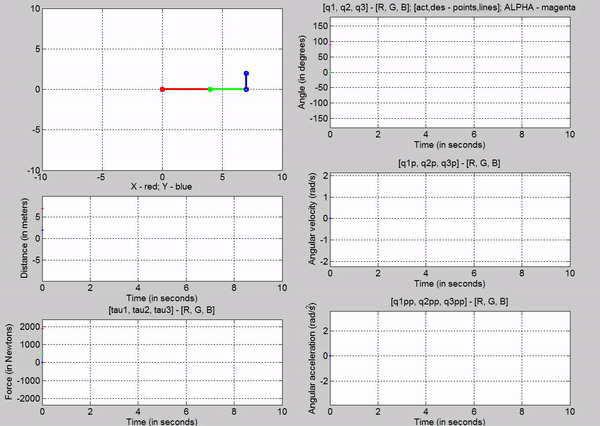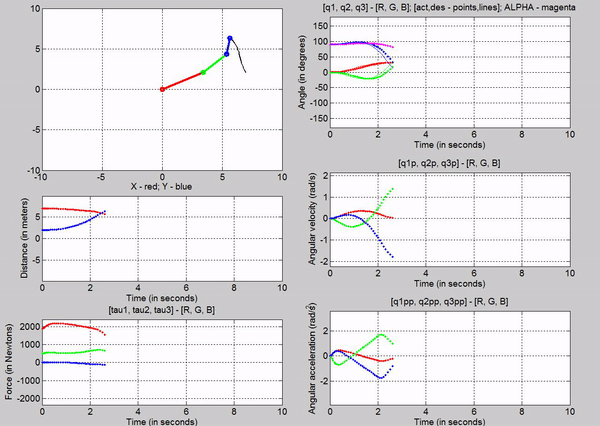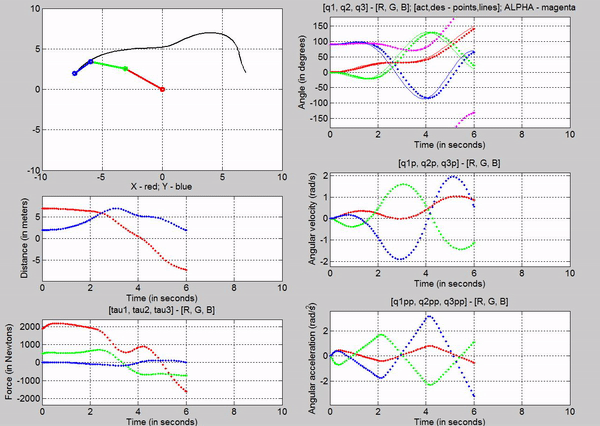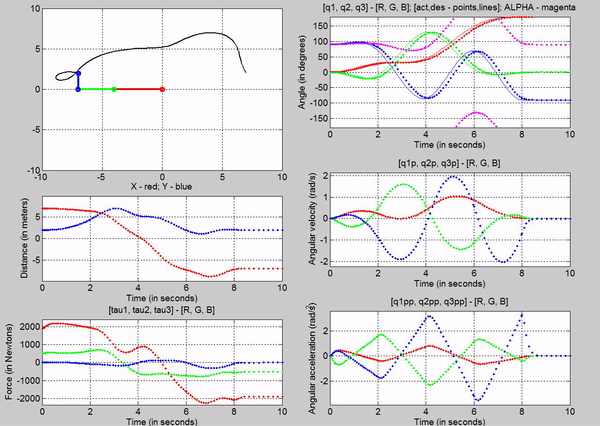
Figure 17: Animation with MATLAB's spline function

We can observe that the simulation using the MATLAB�s function is smoother, i.e., have steadier position slopes. We can also see that the velocity profiles are not as abrupt as the one using the signal builder.

Does the simulation make it to the end?

Yes

Does the value of the selected gains (Kp and Kv) change the simulation?

Ofcourse. The following animation has a Kp of 1 and a Kv of 2:

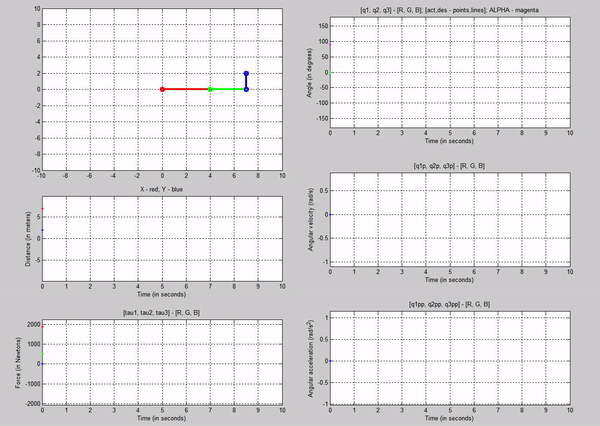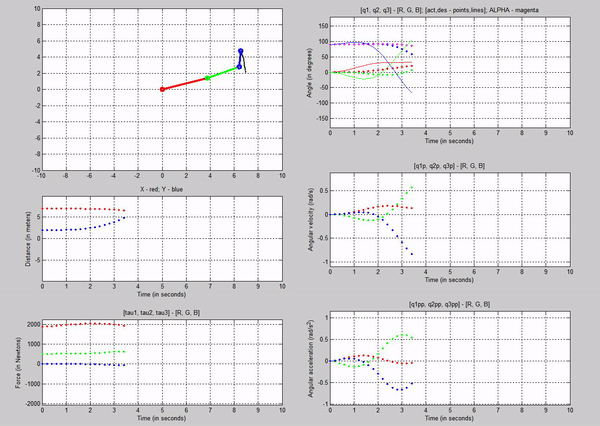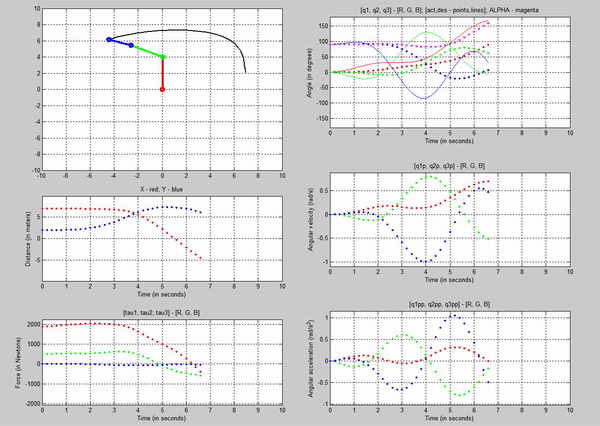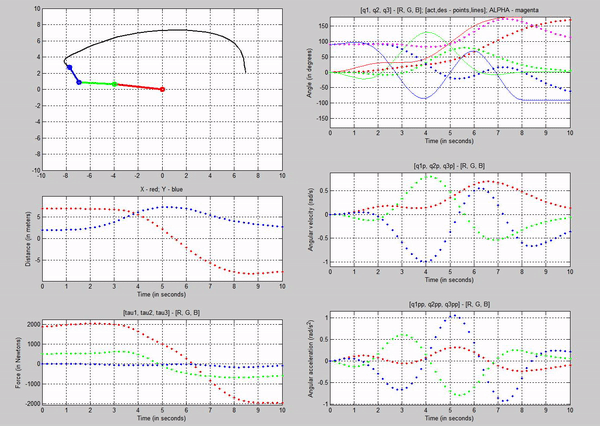
Figure 18: Trajectory follower with Kp=1 and Kv = 2

We notice that there is a large error between the desired and actual joint angles. This is because of the small Kp.

Does the actual path follow the designed trajectory?

It does not exactly follow the desired q angles between the set points at 2, 4, 6 and 8 seconds. However, Kp and Kv can be tuned to achieve it.

 

 

Bonus

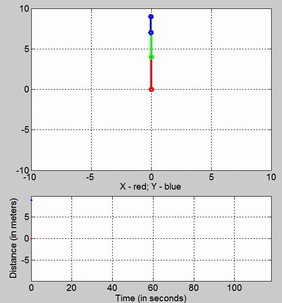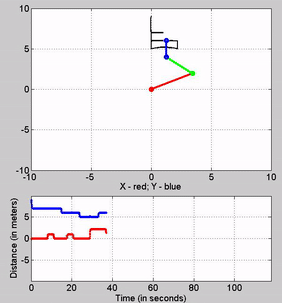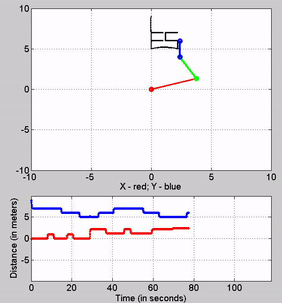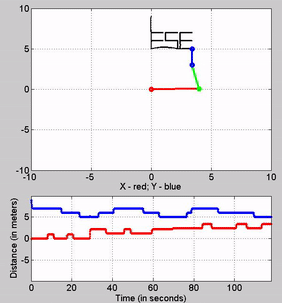
Figure 19: My attempt at writing ESE with the robot